Roadmap

快速处理区间加减问题-前缀和、二维前缀和与差分
前言
在了解二维前缀和之前,我们首先需要了解一下什么是前缀和。
如果我给你一串长度为n的数列a1,a2,a3……an,再给出m个询问,每次询问给出L,R两个数,要求给出区间[L,R]里的数的和,你会怎么做,若是没有了解过前缀和的人看到这道题的想法可能是对于m次询问,我每次都遍历一遍它给的区间,计算出答案,这样子的方法固然没错,但是其时间复杂度达到了O(n*m),如果数据量稍微大一点就有可能超时,而我们如果使用前缀和的方法来做的话就能够将时间复杂度降到O(n+m),大大节省了运算时间。至于怎么用,请看下面一小段代码
1 | a[0]=0; |
没错,前缀和顾名思义就是前面i个数的总和。数组a在经过这样的操作之后,对于每次的询问,我们只需要计算a[R]-a[L-1]就能得到我们想要的答案了,是不是很简单呢。
在知道了最简单的前缀和之后,我们再来了解一下什么是差分。
给你一串长度为n的数列a1,a2,a3……an,要求对a[L]~a[R]进行m次操作:
操作一:将a[L]~a[R]内的元素都加上P
操作二:将a[L]~a[R]内的元素都减去P
最后再给出一个询问求a[L]-a[R]内的元素之和?
你会怎么做呢?你可能会想,我对于m次操作每次都遍历一遍a[L]~a[R],给区间里的数都加上P或减去P,最后再求一次前缀和就行了。没错,这样子确实也能得出正确答案,但时间复杂度却高达O(M*n),对于1<=n,m<=1e5这个数据范围来说直接就tle了,所以说这个方法不可行。既然这样不行的话,那我们要怎么做才能快速的得到正确答案呢?是的,这个时候我们的差分就该派上用场了,我们新开一个数组b,储存每一次的修改操作,最后求前缀和的时候统计一下就能快速的得到正确答案了,详细请看下面代码。
1 | int maxn = 1e5+9; |
相信看到这里,大家已经仔细思考过代码了,为什么操作一时b[R+1]要减去p,很简单,因为操作一我只需对[L,R]区间里的数加p,[R+1,n]这个区间里的数没必要加p,所以需要减掉p。
差分讲解完毕,接下来我们终于要开始今天的正题——二维前缀和了。
总结
- 对于已知有n个元素的数列A[1~n],我们可以建立记录它每项与前一项的差值的差分数组B:显然:B[1]=A[1]-0;对于整数i∈[2,n],取A[i]-A[i-1]为其差分数组B[i]的值

- 性质
- 计算数列各项的值:可以发现数列A的第i项的值是可以用其差分数组B的前n项和计算,即A[i]=∑Bj
- 计算数列的前缀和:第i项的前缀和即为数列前i项的和,那么推导可知
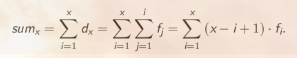
- 计算数列的前缀和:第i项的前缀和即为数列前i项的和,那么推导可知
- 计算数列各项的值:可以发现数列A的第i项的值是可以用其差分数组B的前n项和计算,即A[i]=∑Bj
- 用途
- 快速处理区间加减操作:如果进行区间加减操作,且修改的区间连续,那么若将[x,y]区间内A[i]各加val,我们就可以只对其差分数组B的x和y这两项进行修改,x项B[x]加val ,y项 B[y+1]减val。
- 询问区间和问题:在保证(1)正确修改的基础上,我们可以由性质(2)计算出数列各项的前缀和数组sum各项的值;那么显然,区间[L,R]的和即A[L]+…+A[R] = ans = sum[R]-sum[L-1].
二维
还是以小问题的形式来讲解二维前缀和吧。
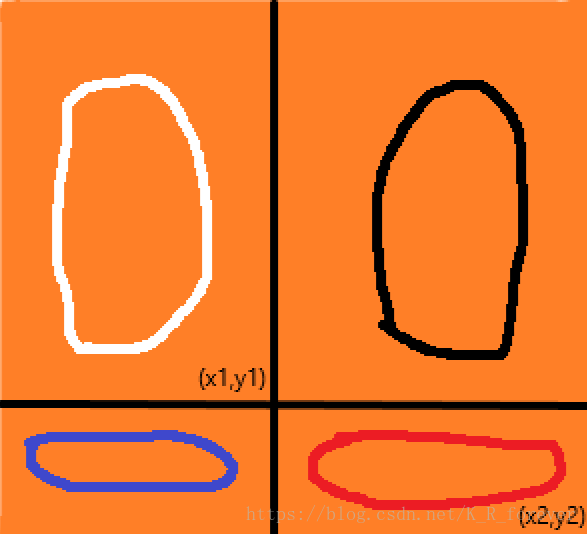
给定一个n*m大小的矩阵a,有q次询问,每次询问给定x1,y1,x2,y2四个数,求以(x1,y1)为左上角坐标和(x2,y2)为右下角坐标的子矩阵的所有元素和。注意仍然包含左上角和右下角的元素。
怎么做呢?为了方便你们理解,我画个图吧。
图画的很丑,希望不要介意。如图所示,按题目要求,我们每次要求的答案就是红色圆圈所在的区域的值(注意,这里的x1,x2表示行,y1,y2表示列),对比上面这张图我们能够发现红色区域的值等于四个区域的值减去(白色区域+黑色区域),再减去(白色区域+蓝色区域),最后因为白色区域被减了两次,我们需要再加回来。所以ans=a[x2][y2]-a[x1-1][y2]-a[x2][y1-1]+a[x1-1][y1-1];(注意,此时的a数组代表的是前缀和)。突然想起来还没说怎么求二维前缀和,很简单,看下面代码。
1 | for(int i=1;i<=n;i++){ |
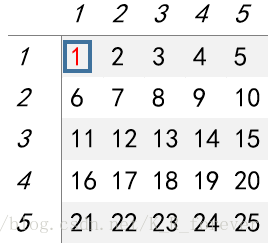
为方便理解贴个图
假如我想求a[2][4]的前缀和,我得先加上a[1][4]的前缀和,再加上a[2][3]的前缀和,然后这个时候我们发现实际上a[1][3]这个部分我们加了两遍,所以我们需要再减去一遍a[1][3],于是得出公式a[i][j]+=a[i][j-1]+a[i-1][j]-a[i-1][j-1]。
接下来看完整代码吧。
1 | #include<bits/stdc++.h> |
是不是感觉很简单呢,哈哈哈哈哈哈哈。
在学完二维前缀和之后,一些同学可能会有疑问,一维前缀和能用上差分,那么二维前缀和能不能用上差分呢?答案是肯定的。
差分
那么怎么差分呢?方法是和一维类似的,我们也是需要另开一个数组记录修改操作,最后求前缀和时统计修改操作,只是二维每一次操作需要记录4个位置,一维只需要记录2个位置。具体怎么做,看下面代码吧。
1 | for(int i=0;i<m;i++){//m是修改操作次数 |
好了,一维前缀和、二维前缀和、差分都说完了,希望看这篇文章的人能够有所收获吧。
二分查找细节分析
思路
我相信对很多读者朋友来说,编写二分查找的算法代码属于玄学编程,虽然看起来很简单,就是会出错,要么会漏个等号,要么少加个 1。
不要气馁,因为二分查找其实并不简单。看看 Knuth 大佬(发明 KMP 算法的那位)怎么说的:
Although the basic idea of binary search is comparatively straightforward,
the details can be surprisingly tricky…
这句话可以这样理解:思路很简单,细节是魔鬼。很多人喜欢拿整型溢出的 bug 说事儿,但是二分查找真正的坑根本就不是那个细节问题,而是在于到底要给 mid 加一还是减一,while 里到底用 <= 还是 <
你要是没有正确理解这些细节,写二分肯定就是玄学编程,有没有 bug 只能靠菩萨保佑。我特意写了一首诗来歌颂该算法,概括本文的主要内容,建议保存:
本文以问答的形式,探究几个最常用的二分查找场景:寻找一个数. 寻找左侧边界. 寻找右侧边界。第一个场景是最简单的算法形式,解决 这道题,后两个场景就是本题。
本文就来探究几个最常用的二分查找场景:寻找一个数. 寻找左侧边界. 寻找右侧边界。而且,我们就是要深入细节,比如不等号是否应该带等号,mid 是否应该加一等等。分析这些细节的差异以及出现这些差异的原因,保证你能灵活准确地写出正确的二分查找算法。
零-二分查找框架
1 | int binarySearch(int[] nums, int target) { |
分析二分查找的一个技巧是:不要出现 else,而是把所有情况用 else if 写清楚,这样可以清楚地展现所有细节。本文都会使用 else if,旨在讲清楚,读者理解后可自行简化。
其中 … 标记的部分,就是可能出现细节问题的地方,当你见到一个二分查找的代码时,首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。
另外声明一下,计算 mid 时需要防止溢出,代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同,但是有效防止了 left 和 right 太大直接相加导致溢出。
一-寻找一个数(基本的二分搜索)
这个场景是最简单的,肯能也是大家最熟悉的,即搜索一个数,如果存在,返回其索引,否则返回 -1。
1 | int binarySearch(int[] nums, int target) { |
- 为什么 while 循环的条件中是 <=,而不是 <?
答:因为初始化 right 的赋值是 nums.length - 1,即最后一个元素的索引,而不是 nums.length。
这二者可能出现在不同功能的二分查找中,区别是:前者相当于两端都闭区间 [left, right],后者相当于左闭右开区间 [left, right),因为索引大小为 nums.length 是越界的。
我们这个算法中使用的是前者 [left, right] 两端都闭的区间。这个区间其实就是每次进行搜索的区间。
什么时候应该停止搜索呢?当然,找到了目标值的时候可以终止:
1 | if(nums[mid] == target) return mid; |
但如果没找到,就需要 while 循环终止,然后返回 -1。那 while 循环什么时候应该终止?搜索区间为空的时候应该终止,意味着你没得找了,就等于没找到嘛。
while(left <= right) 的终止条件是 left == right + 1,写成区间的形式就是 [right + 1, right],或者带个具体的数字进去 [3, 2],可见这时候区间为空,因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的,直接返回 -1 即可。
while(left < right) 的终止条件是 left == right,写成区间的形式就是 [left, right],或者带个具体的数字进去 [2, 2],这时候区间非空,还有一个数 2,但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了,索引 2 没有被搜索,如果这时候直接返回 -1 就是错误的。
当然,如果你非要用 while(left < right) 也可以,我们已经知道了出错的原因,就打个补丁好了:
1 | //... |
为什么 left = mid + 1,right = mid - 1?我看有的代码是 right = mid 或者 left = mid,没有这些加加减减,到底怎么回事,怎么判断?
答:这也是二分查找的一个难点,不过只要你能理解前面的内容,就能够很容易判断。
刚才明确了「搜索区间」这个概念,而且本算法的搜索区间是两端都闭的,即 [left, right]。那么当我们发现索引 mid 不是要找的 target 时,下一步应该去搜索哪里呢?
当然是去搜索 [left, mid-1] 或者 [mid+1, right] 对不对?因为 mid 已经搜索过,应该从搜索区间中去除。此算法有什么缺陷?
答:至此,你应该已经掌握了该算法的所有细节,以及这样处理的原因。但是,这个算法存在局限性。
比如说给你有序数组 nums = [1,2,2,2,3],target 为 2,此算法返回的索引是 2,没错。但是如果我想得到 target 的左侧边界,即索引 1,或者我想得到 target 的右侧边界,即索引 3,这样的话此算法是无法处理的。
这样的需求很常见,你也许会说,找到一个 target,然后向左或向右线性搜索不行吗?可以,但是不好,因为这样难以保证二分查找对数级的复杂度了。
我们后续的算法就来讨论这两种二分查找的算法。
二-寻找左侧边界的二分搜索
以下是最常见的代码形式,其中的标记是需要注意的细节:
1 | int left_bound(int[] nums, int target) { |
为什么 while 中是 < 而不是 <=?
答:用相同的方法分析,因为 right = nums.length 而不是 nums.length - 1。因此每次循环的「搜索区间」是 [left, right) 左闭右开。
while(left < right) 终止的条件是 left == right,此时搜索区间 [left, left) 为空,所以可以正确终止。
PS:这里先要说一个搜索左右边界和上面这个算法的一个区别,也是很多读者问的:刚才的 right 不是 nums.length - 1 吗,为啥这里非要写成 nums.length 使得「搜索区间」变成左闭右开呢?
因为对于搜索左右侧边界的二分查找,这种写法比较普遍,我就拿这种写法举例了,保证你以后遇到这类代码可以理解。你非要用两端都闭的写法反而更简单,我会在后面写相关的代码,把三种二分搜索都用一种两端都闭的写法统一起来,你耐心往后看就行了。为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办?

答:因为要一步一步来,先理解一下这个「左侧边界」有什么特殊含义:
对于这个数组,算法会返回 1。这个 1 的含义可以这样解读:nums 中小于 2 的元素有 1 个。
比如对于有序数组 nums = [2,3,5,7], target = 1,算法会返回 0,含义是:nums 中小于 1 的元素有 0 个。
再比如说 nums = [2,3,5,7], target = 8,算法会返回 4,含义是:nums 中小于 8 的元素有 4 个。
综上可以看出,函数的返回值(即 left 变量的值)取值区间是闭区间 [0, nums.length],所以我们简单添加两行代码就能在正确的时候 return -1:
1 | while (left < right) { |
- 为什么 left = mid + 1,right = mid ?和之前的算法不一样?
答:这个很好解释,因为我们的「搜索区间」是 [left, right) 左闭右开,所以当 nums[mid] 被检测之后,下一步的搜索区间应该去掉 mid 分割成两个区间,即 [left, mid) 或 [mid + 1, right)。 - 为什么该算法能够搜索左侧边界?
答:关键在于对于 nums[mid] == target 这种情况的处理:
1 | if (nums[mid] == target) |
可见,找到 target 时不要立即返回,而是缩小「搜索区间」的上界 right,在区间 [left, mid) 中继续搜索,即不断向左收缩,达到锁定左侧边界的目的。
为什么返回 left 而不是 right?
答:都是一样的,因为 while 终止的条件是 left == right。能不能想办法把 right 变成 nums.length - 1,也就是继续使用两边都闭的「搜索区间」?这样就可以和第一种二分搜索在某种程度上统一起来了。
答:当然可以,只要你明白了「搜索区间」这个概念,就能有效避免漏掉元素,随便你怎么改都行。下面我们严格根据逻辑来修改:
因为你非要让搜索区间两端都闭,所以 right 应该初始化为 nums.length - 1,while 的终止条件应该是 left == right + 1,也就是其中应该用 <=:
1 | int left_bound(int[] nums, int target) { |
因为搜索区间是两端都闭的,且现在是搜索左侧边界,所以 left 和 right 的更新逻辑如下:
1 | if (nums[mid] < target) { |
由于 while 的退出条件是 left == right + 1,所以当 target 比 nums 中所有元素都大时,会存在以下情况使得索引越界: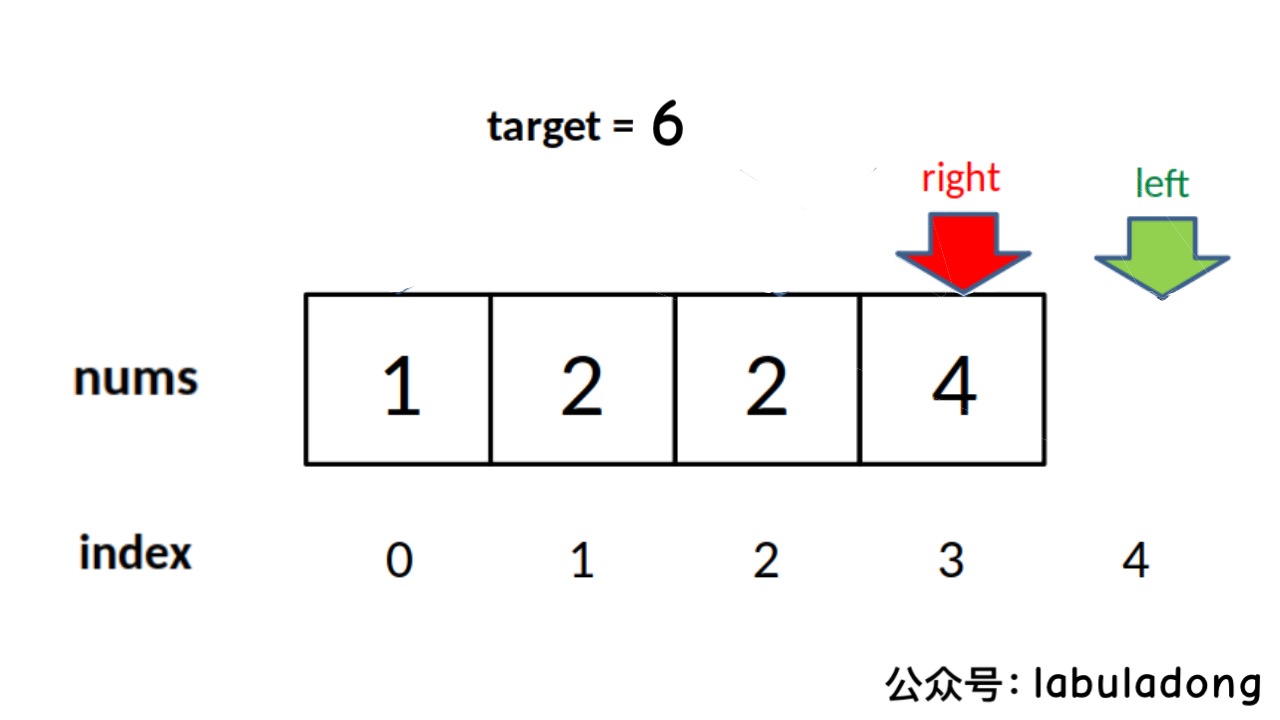
因此,最后返回结果的代码应该检查越界情况:
1 | if (left >= nums.length || nums[left] != target) |
至此,整个算法就写完了,完整代码如下:
1 | int left_bound(int[] nums, int target) { |
这样就和第一种二分搜索算法统一了,都是两端都闭的「搜索区间」,而且最后返回的也是 left 变量的值。只要把住二分搜索的逻辑,两种形式大家看自己喜欢哪种记哪种吧。
三-寻找右侧边界的二分查找
类似寻找左侧边界的算法,这里也会提供两种写法,还是先写常见的左闭右开的写法,只有两处和搜索左侧边界不同,已标注:
1 | int right_bound(int[] nums, int target) { |
- 为什么这个算法能够找到右侧边界?
答:类似地,关键点还是这里:
1 | if (nums[mid] == target) { |
当 nums[mid] == target 时,不要立即返回,而是增大「搜索区间」的下界 left,使得区间不断向右收缩,达到锁定右侧边界的目的。
- 为什么最后返回 left - 1 而不像左侧边界的函数,返回 left?而且我觉得这里既然是搜索右侧边界,应该返回 right 才对。
答:首先,while 循环的终止条件是 left == right,所以 left 和 right 是一样的,你非要体现右侧的特点,返回 right - 1 好了。
至于为什么要减一,这是搜索右侧边界的一个特殊点,关键在这个条件判断:
1 | if (nums[mid] == target) { |

因为我们对 left 的更新必须是 left = mid + 1,就是说 while 循环结束时,nums[left] 一定不等于 target 了,而 nums[left-1] 可能是 target。
至于为什么 left 的更新必须是 left = mid + 1,同左侧边界搜索,就不再赘述。
- 为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办?
答:类似之前的左侧边界搜索,因为 while 的终止条件是 left == right,就是说 left 的取值范围是 [0, nums.length],所以可以添加两行代码,正确地返回 -1:
1 | while (left < right) { |
- 是否也可以把这个算法的「搜索区间」也统一成两端都闭的形式呢?这样这三个写法就完全统一了,以后就可以闭着眼睛写出来了。
答:当然可以,类似搜索左侧边界的统一写法,其实只要改两个地方就行了:
1 | int right_bound(int[] nums, int target) { |
当 target 比所有元素都小时,right 会被减到 -1,所以需要在最后防止越界:
至此,搜索右侧边界的二分查找的两种写法也完成了,其实将「搜索区间」统一成两端都闭反而更容易记忆,你说是吧?
四-逻辑统一
来梳理一下这些细节差异的因果逻辑:
第一个,最基本的二分查找算法:
因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1
因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回第二个,寻找左侧边界的二分查找:
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界第三个,寻找右侧边界的二分查找:
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid
因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界
又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right,必须减一
对于寻找左右边界的二分搜索,常见的手法是使用左闭右开的「搜索区间」,我们还根据逻辑将「搜索区间」全都统一成了两端都闭,便于记忆,只要修改两处即可变化出三种写法:
1 | int binary_search(int[] nums, int target) { |
如果以上内容你都能理解,那么恭喜你,二分查找算法的细节不过如此。
通过本文,你学会了:
- 分析二分查找代码时,不要出现 else,全部展开成 else if 方便理解。
- 注意「搜索区间」和 while 的终止条件,如果存在漏掉的元素,记得在最后检查。
- 如需定义左闭右开的「搜索区间」搜索左右边界,只要在 nums[mid] == target 时做修改即可,搜索右侧时需要减一。
- 如果将「搜索区间」全都统一成两端都闭,好记,只要稍改 nums[mid] == target 条件处的代码和返回的逻辑即可,推荐拿小本本记下,作为二分搜索模板。
最后,点击我的头像可以查看更多详细题解,希望读者多多点赞,让我感受到你的认可~ - 推荐阅读:
- 回溯算法详解
- KMP 算法详解
- LRU 缓存淘汰算法详解
- 腾讯面试题详解:编辑距离
PS:我的所有算法文章都已经上传到了 Github 仓库:fucking-algorithm,共 60 多篇,绝对精品,肯定让你收获满满,求个 star 不过分吧~
PPS:我最近精心制作了一份电子书《labuladong的算法小抄》,分为「动态规划」「数据结构」「算法思维」「高频面试」四个章节,目录如下,如有需要可扫码到我的公众号 labuladong 后台回复关键词「pdf」下载:
作者:labuladong
链接:https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/solution/er-fen-cha-zhao-suan-fa-xi-jie-xiang-jie-by-labula/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处